Bubble Sort

Bubble Sort Algorithm

Introduction

Bubble Sort is one of the simplest sorting algorithms available. It’s frequently used as an introductory algorithm to help new programmers understand the concept of algorithmic sorting.

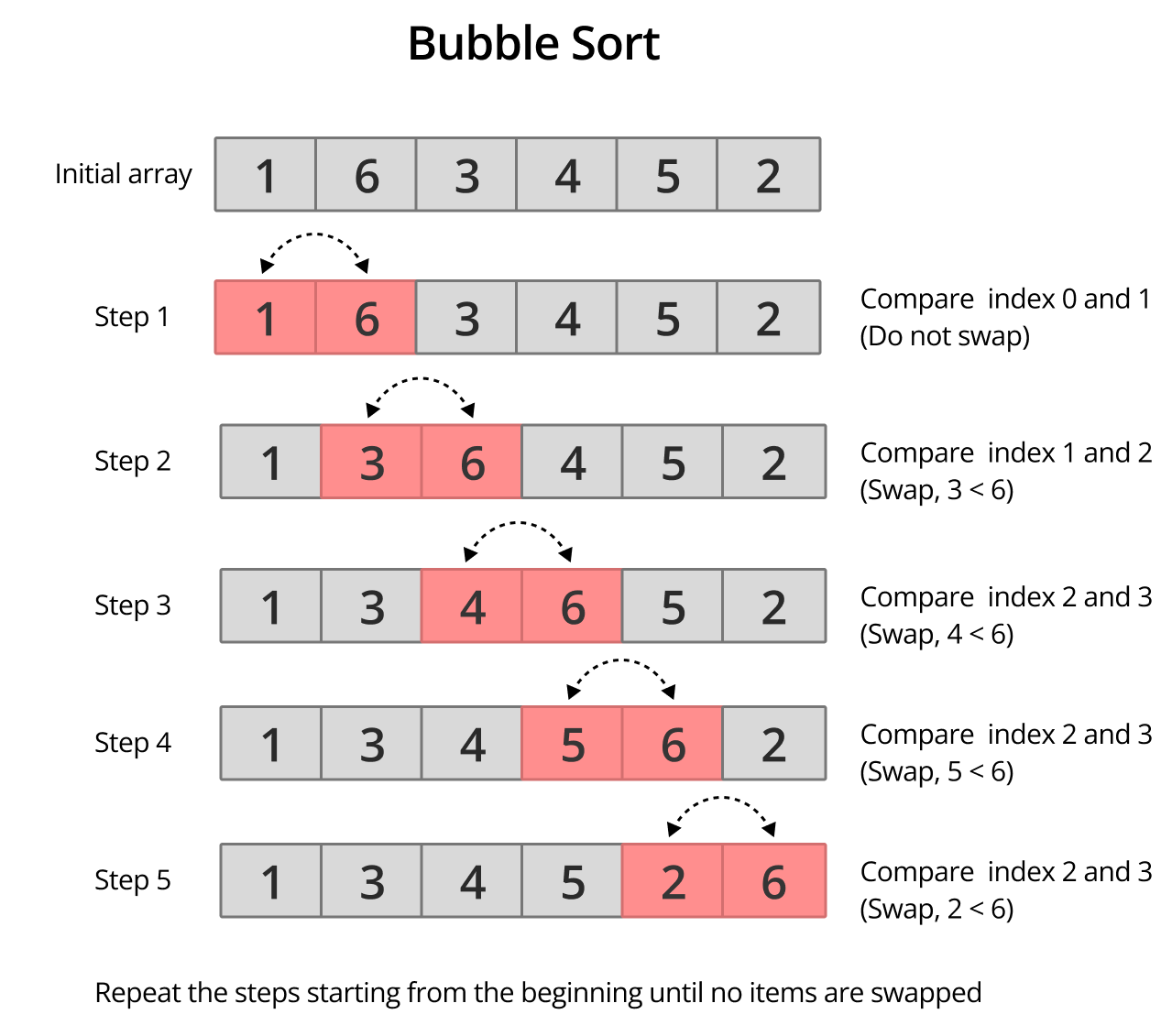
Explanation

Bubble Sort works by repeatedly stepping through the list to be sorted, comparing each pair of adjacent items, and swapping them if they are in the wrong order. The process is repeated until no swaps are needed, indicating that the list is sorted.

JavaScript Implementation

	function bubbleSort(arr) {
	  let n = arr.length;
	  // Flag used to determine if a swap occurred
	  let swapped;
	  do {
	    swapped = false;
	    for (let i = 0; i < n - 1; i++) {
	      if (arr[i] > arr[i + 1]) {
	        // Swap the elements
	        let temp = arr[i];
	        arr[i] = arr[i + 1];
	        arr[i + 1] = temp;
	        swapped = true;
	      }
	    }
	  } while (swapped);
	  return arr;
	}
	// Example: bubbleSort([29, 72, 98, 13, 87]);

Pros and Cons

• Pros:
  • Simple to understand and implement.
  • Useful for small datasets or as an educational tool.
• Cons:
  • Inefficient for large datasets with a time complexity of (O(n^2)).
  • Often outperformed by more complex algorithms in practical use.

Time Complexity

• Worst and Average Case: (O(n^2)) where (n) is the number of items being sorted.
• Best Case (when the list is already sorted): (O(n)).

Space Complexity

• Constant Space Complexity: (O(1)), as it only uses a fixed amount of extra memory space.

Practical Use Cases

• Educational purposes to demonstrate basic sorting.
• Suitable for small datasets where simplicity is more valuable than efficiency.

Variations or Related Algorithms

• Optimized Bubble Sort: Includes a flag to stop the algorithm if the array gets sorted before all passes are completed.
• Cocktail Shaker Sort: A variation that sorts in both directions on each pass through the list.

Conclusion

Bubble Sort, with its simplicity and ease of implementation, serves as an excellent starting point for understanding sorting algorithms. However, its inefficiency with large datasets limits its practical use to smaller arrays or educational contexts.