What is BigO Notation?
The Concept of BigO Notation
BigO notation is a mathematical concept used in computer science to describe the performance of an algorithm. In simpler terms, it’s a way to express how the runtime of an algorithm grows relative to the input size. This concept is crucial for developers to understand the efficiency of different approaches to solving problems.
Time Complexity and Space Complexity
BigO notation primarily deals with two types of complexities:
Time Complexity: This measures how the execution time of an algorithm increases with the size of the input data. It’s essential for understanding how fast or slow an algorithm performs.
Space Complexity: This refers to the amount of memory space required by an algorithm as the input size grows. While less frequently discussed than time complexity, it’s equally important, especially in environments with limited memory resources.
Why BigO Notation Is Used
BigO notation provides a high-level understanding of the algorithm without getting bogged down in machine-specific details. It allows developers to compare the efficiency of different algorithms and choose the most appropriate one for their needs.
BigO Complexity Classes
BigO notation categorizes algorithms into different classes based on their performance characteristics. The most common classes are:
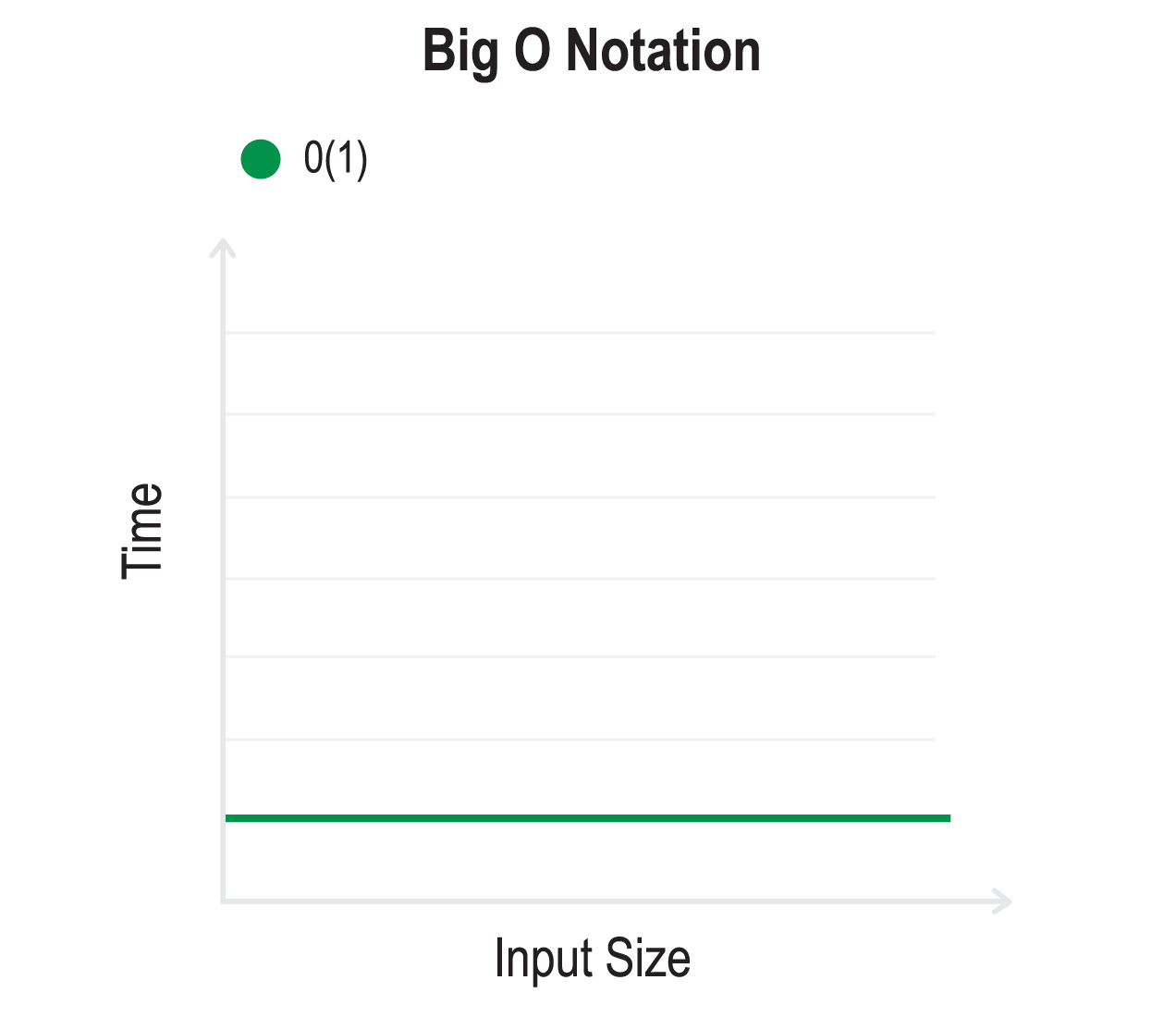
- O(1) - Constant Time: The execution time remains constant, regardless of the input size.
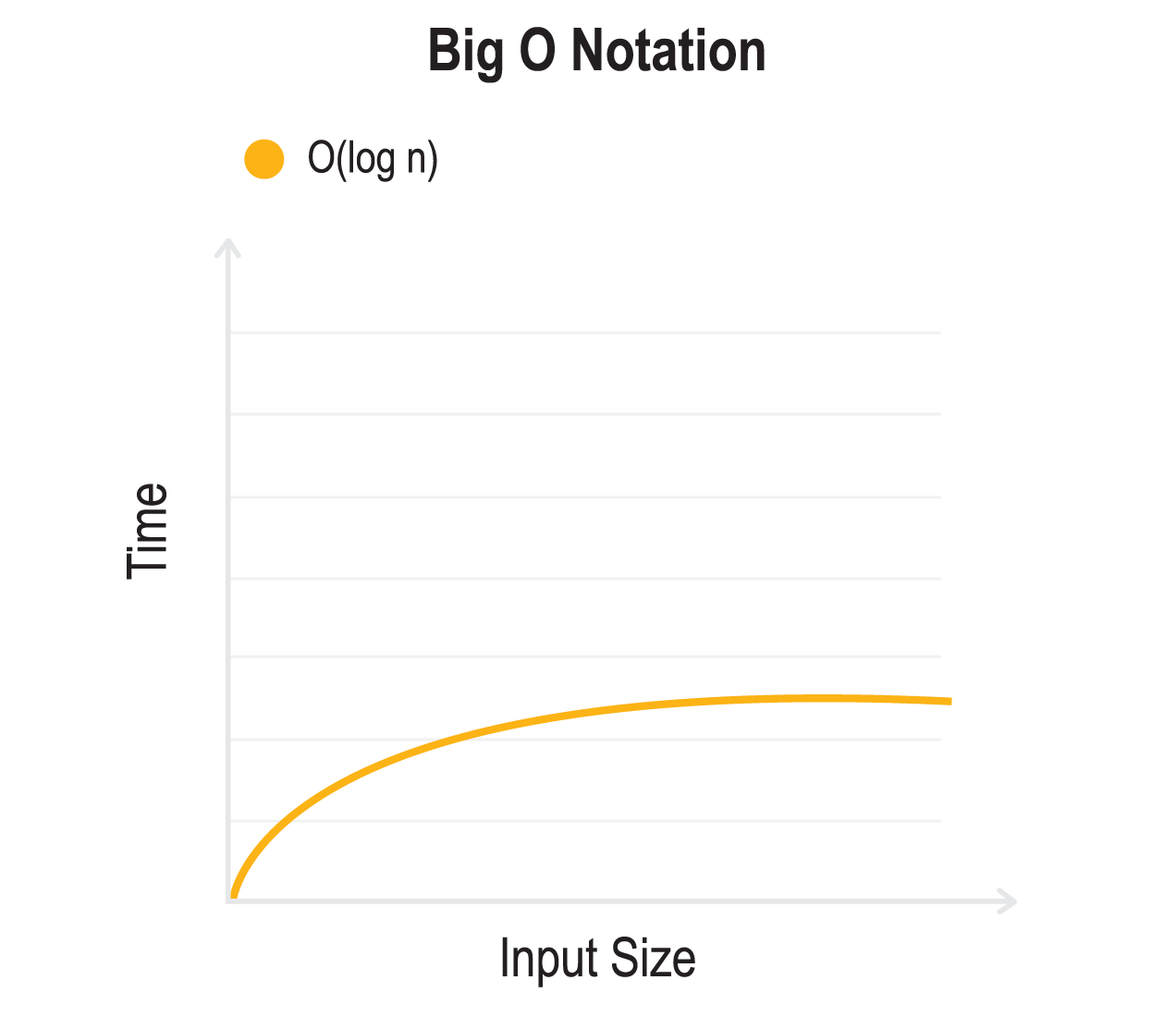
- O(log n) - Logarithmic Time: The execution time grows logarithmically with the input size.
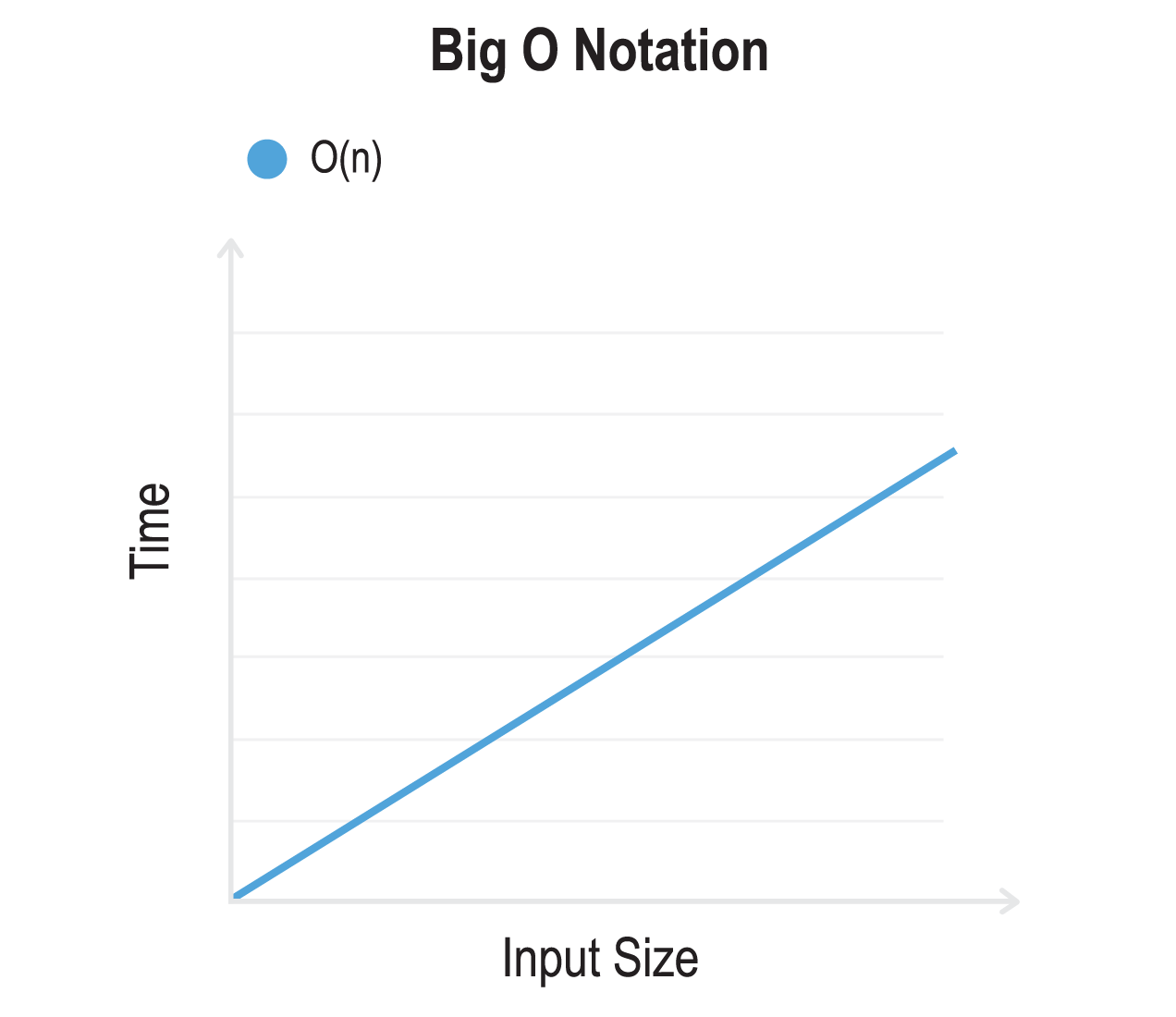
- O(n) - Linear Time: The execution time grows linearly with the input size.
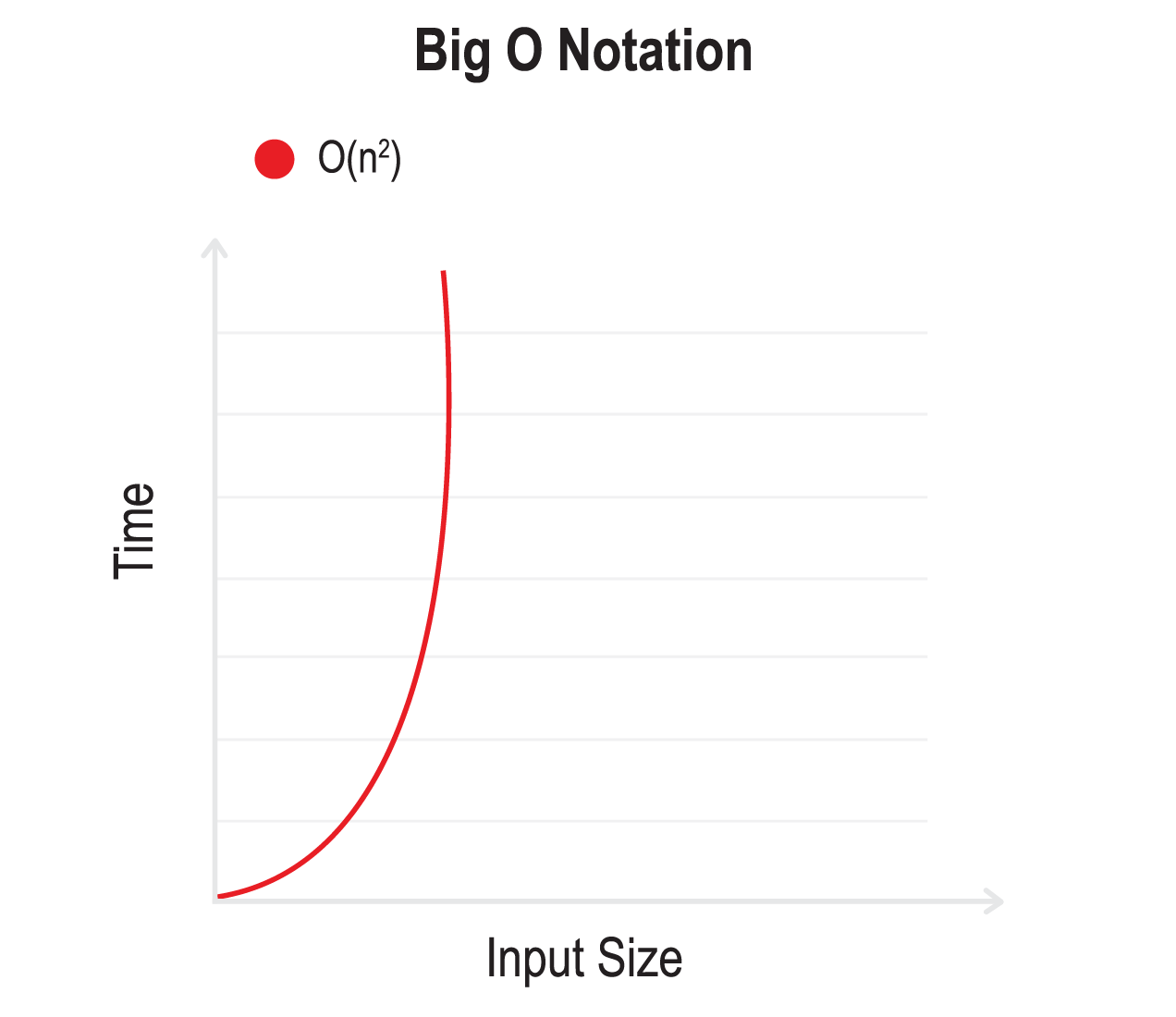
- O(n^2) - Quadratic Time: The execution time grows quadratically with the input size.
O(2^n) - Exponential Time: The execution time grows exponentially with the input size.
O(n!) - Factorial Time: The execution time grows factorially with the input size.
Real-World Analogy
Think of BigO notation like a recipe. The complexity of a recipe (algorithm) can vary depending on the number of ingredients (input size). A recipe that requires a constant number of steps, no matter how many guests (input size) you’re cooking for, is like O(1). In contrast, a recipe where the steps double with each additional guest is more like O(2^n).
Conclusion
Understanding BigO notation is a key skill in a developer’s toolbox, especially for JavaScript developers looking to optimize web applications for performance and efficiency. As we delve into each type of BigO notation in the following sections, we’ll provide detailed explanations and practical JavaScript examples to illustrate these concepts.